Professor Yinyu Ye is currently giving a lecture series on Optimization Methods for Data Science, Machine Learning, and AI at the Shanghai Institute for Mathematical and Interdisciplinary Sciences (SIMIS). This week’s lecture—part two of the series—is focused on duality.
Lecture videos and course materials are available here: https://www.simis.cn/optimization-methods-for-data-science-and-machine-learning-and-ai/
The class style is really “minimalistic examples for profound insights.” There’s a similar phrase often used in China: 大道至简 (The greatest truths are the simplest). It may sound cliché, but a contribution so widely-known that it becomes a cliché—that’s impact, lol.
Anyway:
1. Infeasibility certificate
Let’s start with a classic. To prove the infeasibility of a linear system: $$ Ax =0, \quad x\ge 0 $$ One can rewrite it as an LP: $$ \text{Primal}\qquad \begin{align*} \min \ & 0^T x\cr s.t.\ & Ax = b\cr &x\ge 0 \end{align*} $$ Its dual is $$ \text{Dual}\qquad \begin{align*} \max \ & b^T y\cr s.t.\ & A^T y \le 0 \end{align*} $$ According to the strong duality theorem, the primal is infeasible if and only if the dual is unbounded. In this case, the dual is unbounded if there exists a $y \neq 0$ such that $A^T y \le 0$. $y$ here is an infeasibility certificate for the linear system.
This is Farka’s Lemma for linear system. But it would take a much more cumbersome efforts to prove it otherwise.
2. Dual with slack variables
Let’s now consider a slight generalization to Conic Linear Programming (a natural extension of LP). Suppose we replace the non-negativity constraint $x \ge 0$ with $x \in K$, where $K$ is a cone (a set closed under non-negative scaling).
The Primal problem becomes:
$$ \begin{aligned} \min \quad & c^T x \ \text{s.t.} \quad & A x = b \ & x \in K \end{aligned} $$
The dual of this conic LP is elegantly formulated by introducing dual variables $y \in \mathbb{R}^{\text{col}(A)}$ and slack variables $s \in \mathbb{R}^{\text{col}(A)}$:
$$ \begin{aligned} \max \quad & b^T y \ \text{s.t.} \quad & A^T y + s = c \ & s \in K^* \end{aligned} $$
Here, $K^*$ is the dual cone of $K$, and a crucial property is that the dual cone of any cone is always convex. This closely resembles the well-known result that the Lagrangian of any convex optimization problem is also convex. A similar duality structure appears in Semidefinite Programming (SDP), where the vector product generalizes to the Hadamard product (entrywise multiplication of matrices). Basically, if $C$ and $X$ are matrices $$ \text{vector: }c^Tx \Leftrightarrow \text{matrices: } C\bullet X = \sum_{ij} C_{ij} X_{ij}. $$ It’s like, replacing vector product $\cdot$ with $\bullet$ you can pretend you know SDP duality well to fool your TA in midterms :)
One cool application: the Wasserstein Barycenter Problem
Next up, we see an application of duality in a more concrete setting: the Wasserstein Barycenter Problem. First, let’s introduce the Wasserstein distance.
First we will introduce Wasserstein distance, and a little bit of its properties
Wasserstein Distance
Consider a transportation problem where there’s supply $\mathbf{s}$ and demand $\mathbf{d}$ across a transportation graph, with transportation costs $C$ associated with each edge:
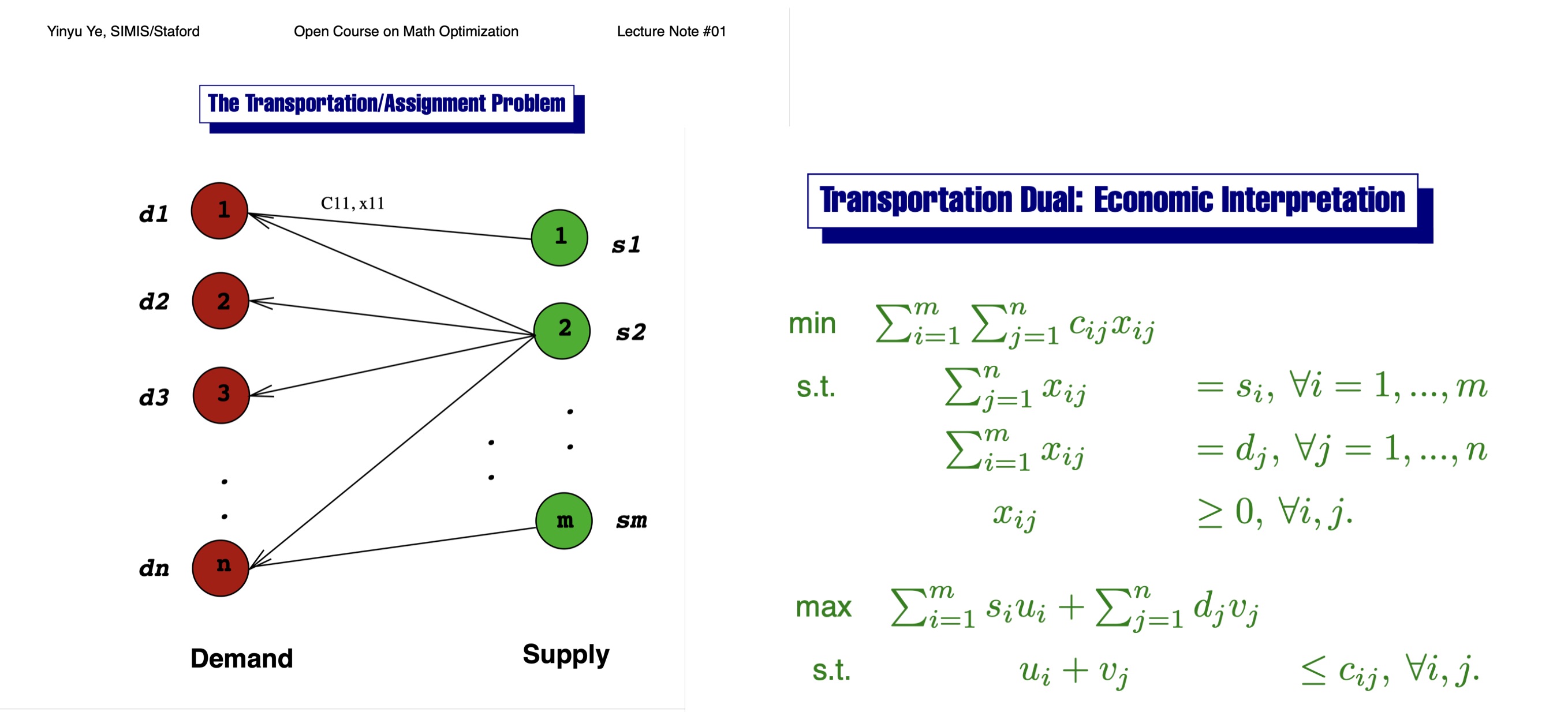
Left: transportation problem/allocation/two-sided matching. Right: its corresponding Primal/Dual.
The Wasserstein distance between the supply $\mathbf{s}$ and demand $\mathbf{d}$ is the minimal transportation cost required to match them. The problem is linear and can be formulated as an LP as shown above.
The interesting part comes from the dual variables. Let’s say we perturb the supply slightly by $\Delta_s$. The change in the objective value will be:
$$ \Delta_s \cdot u $$
where $u$ is the dual variable corresponding to the constraint $\sum_{j=1}^n x_{ij} = s_i$, for all $i$. So, in a sense, $u$ tells us how sensitive the optimal transportation cost is to changes in the supply. Actually, the dual variable $u$ acts as the gradient of the Wasserstein distance with respect to the supply $\mathbf{s}$:
$$ \nabla_{\mathbf{s}} WD_{\mathbf{d}}(\mathbf{s}) = u. $$
Now, let’s level up the problem and introduce randomness into the demand.
Wasserstein Barycenter Problem
Let the demand $\mathbf{d}$ now be a random variable with a prior distribution $\mathbf{d} \sim \mathcal{F}$. Our goal is to find a supply $\mathbf{s}$ that minimizes the expected Wasserstein distance between $\mathbf{s}$ and $\mathbf{d}$, i.e.,
$$ \text{Master Problem:} \quad \mathbb{E}{\mathbf{d} \sim \mathcal{F}}[WD{\mathbf{d}}(\mathbf{s})] $$
Here, $WD_{\mathbf{d}}(\mathbf{s})$ is the Wasserstein distance between a random demand $\mathbf{d}$ and the supply $\mathbf{s}$, exactly, the solution of the transportation LP above. It’s like a child problem.
And in the mater problem, we seek to minimize the overall expected cost, given that $\mathbf d$ is random (subject to, say, linear constraints that ensure $\mathbf{s}$ is a valid transportation plan, for instance, $\sum_i s_i = \sum_j d_j$)
What’s fascinating is that for each fixed $\mathbf{d}$, the dual variable corresponding to the Wasserstein problem can be viewed as the gradient of the objective with respect to $\mathbf{s}$:
$$ \nabla_{\mathbf{s}} WD_{\mathbf{d}}(\mathbf{s}) $$
Which is eactly, the dual variable of the child problem (tranportation LP). With this gradient information we can do a lot then—optimizing w.r.t. gradient-based method, do decentralized parallelization, etc.
Spoiler: next week is zero/first/second-order optimization algorithms. I suspect we will spend a delightful amount of time on Newton/Interior Point methods. Stay tuned~