Always a delight to learn from Professor Ye :) (He was in Shanghai 2023 Winter and I have my LP book signed by him!!!)

Prof. Yinyu Ye teaching at SIMIS. Day one of lectures on optimization and a bit market design.
Professor Yinyu Ye is currently visiting the Shanghai Institute for Mathematical and Interdisciplinary Sciences (SIMIS), delivering a lecture series on Optimization Methods for Data Science, Machine Learning, and AI.
Lecture videos and course materials are available here: https://www.simis.cn/optimization-methods-for-data-science-and-machine-learning-and-ai/
I especially like today’s lecture because there are a lot of simple examples—simplicity is the ultimate sophistication. Professor Ye is such a mater of optimization that all the demo examples are so well-defined that even without the complicate details, they shows the insights. AMAZING.
One particularly elegant example from the course is about Algorithmic Market Design for a World Cup prediction market, modeled as a linear program (LP):
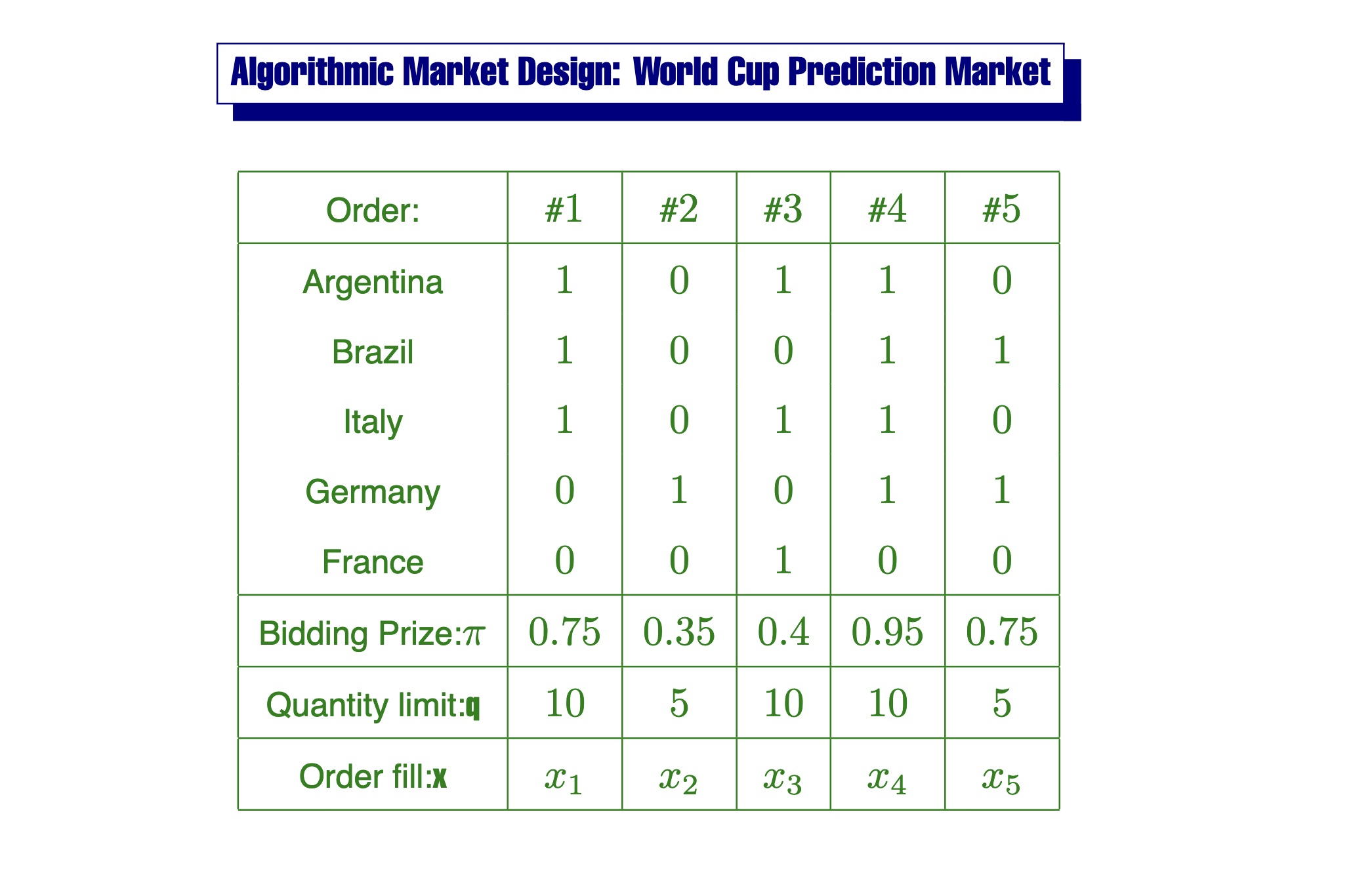
Each bid order corresponds to a bet over possible winners. Bidders submit binary predictions, bidding prices, and quantity limits.
Each bidder bid for their believed countries. If guess correct, they win (normalized) $1. Formalizing the problem with a few more notations:
$V \in {{0, 1}}^{K \times N}$: a binary matrix representing predictions, where $K$ is the number of possible outcomes (e.g. teams), and $N$ is the number of bidders.
- Each column $V_{\cdot j}$ encodes bidder $j$’s prediction: 1s indicate which outcomes they believe are possible.
$\vec{\pi} \in \mathbb{R}^N$: the vector of bidding prices.
$\vec{q} \in \mathbb{R}^N$: the maximum quantity each bidder is willing to buy.
We aim to choose an allocation vector $\vec{x} \in \mathbb{R}^N$, representing how much of each bidder’s order to fill, to maximize worst-case revenue across possible outcomes. This leads to the following LP:
$$ \begin{aligned} \max_{\vec{x},; y} \quad & \vec{\pi}^\top \vec{x} - y \cr \text{s.t.} \quad & V \vec{x} \le \vec{1} \cdot y \cr & \vec{x} \le \vec{q} \cr & \vec{x} \ge 0,\quad y \ge 0 \end{aligned} $$
Interpretation for the LP primal: The term $y$ captures the worst-case payout. The constraint $V\vec{x} \le \vec{1} \cdot y$ ensures that for each outcome (row), the total payoff (across bidders who predicted it) doesn’t exceed $y$.
The dual of this LP is:
$$ \begin{aligned} \min_{\vec{\alpha},; \vec{\beta}} \quad & \vec{q}^\top \vec{\beta} \cr \text{s.t.} \quad & V^\top \vec{\alpha} + \vec{\beta} \ge \vec{\pi} \cr & \vec{1}^\top \vec{\alpha} = 1 \cr & \vec{\alpha} \ge 0,\quad \vec{\beta} \ge 0 \end{aligned} $$
Interpretation of Dual Variables: $\vec{\alpha} \in \mathbb{R}^K$: can be interpreted as a probability distribution over outcomes—according to market-implied belief. $\vec{\beta} \in \mathbb{R}^N$: shadow prices on the quantity limits $\vec{q}$.
Two Key Observations:
Naive averaging isn’t optimal. Simply averaging the binary prediction vectors $V_{\cdot j}$ ignores bidding prices $\vec{\pi}$ and quantity limits $\vec{q}$, both of which encode valuable information.
Market reveals beliefs. The optimal dual variable $\vec{\alpha}$ gives us a market-derived probability distribution—aggregating bidder signals in a principled way via LP duality.