This post is for personal reference and stems from intellectual interest. All credit goes to the original authors; screenshots are from the source. Any errors are mine. Please contact me if you’d like changes—I’m happy to update.
Setup: matrix completion for $n\times m$ $M$ — given an estimator $\hat M$, error is measured as the mean square error: $$ \mathrm{MSE}(\hat M) = \mathbb E[\frac1{mn}\sum_{i, j}(\hat m_{ij} - m_{ij})^2] $$ Setup:

The Universal Singular Value Thresholding (USVT) estimator are:
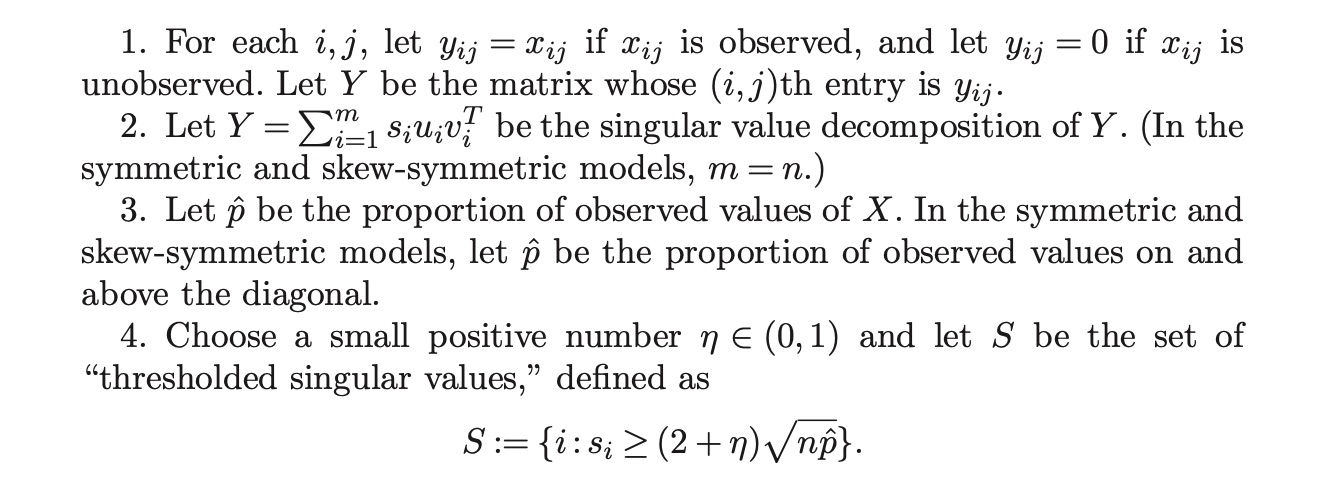
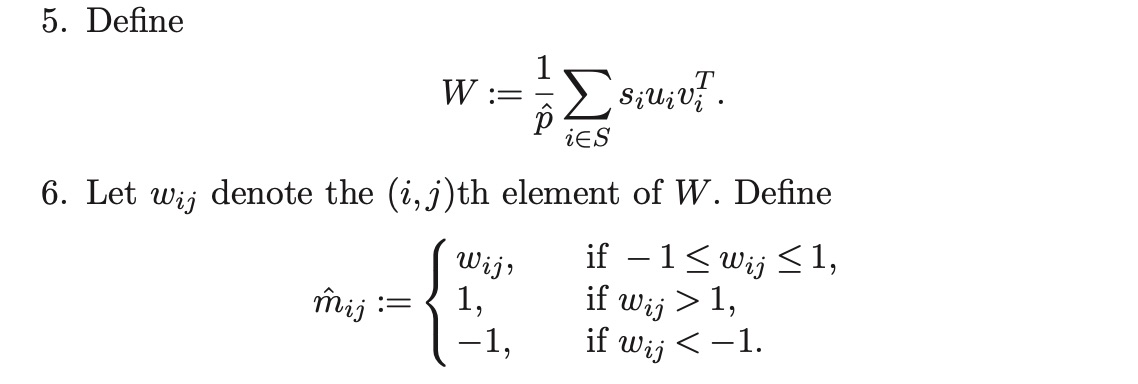
The paper’s coolest part, in my pov, is the following Theorem:
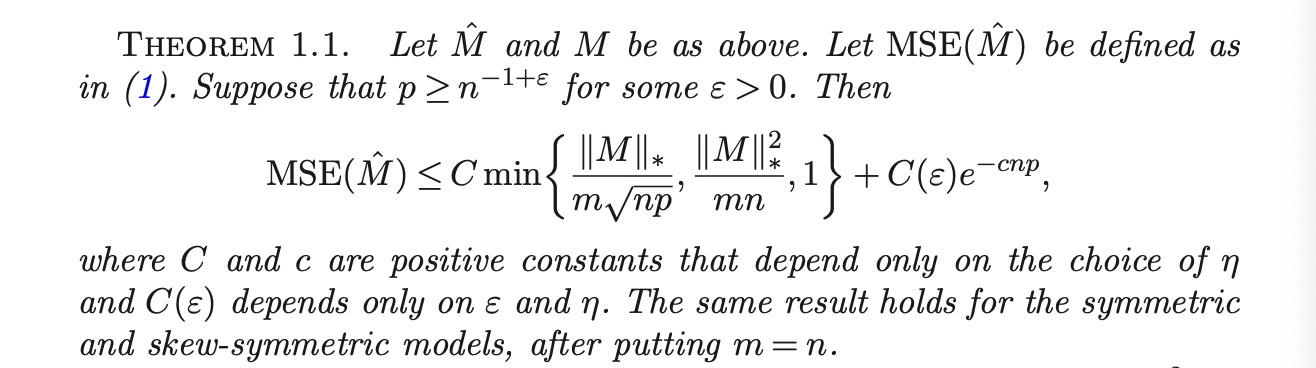
Proof Sketch of Theorem 1.1
First, the proof plays with the following three measures (norms). Let $A$ ($a_{ij}) $be any $m\times n$ matrix, denote $k = \min(m, n)$
Frobenius norm $$ \Vert A\Vert_F = (\sum_{ij} a_{ij}^2)^{1/2} = (\mathrm{Tr} (A^TA))^{\frac12} = (\sum_{i = 1}^k \sigma_i^2)^{\frac12} $$
Nuclear norm $$ \Vert A\Vert_* = \sum_{i = 1}^k \sigma_i $$
Spectral norm $$ \Vert A\Vert = \max_{i\in [k]} |\sigma_i| $$
Back to matrix completions. First, the paper has a key Lemma 3.5. It links the Frobenius norm to the spectral norm and the nuclear norm:
Lemma 3.5 (from the paper) Let $A = \sum_{i = 1}^m \sigma_i x_i y_i^T$ be the SVD of $A$. Fix any $\delta > 0$ and define $\hat B$ — an estimator of $B$ using $A$: $$ \hat B := \sum_{i:\sigma_i > (1 + \delta)\Vert A - B\Vert}\sigma_i x_i y_i^T. $$ Then, $B$ and $\hat B$’s (Frobenius) distance can be related with A and B’s spectral distance and B’s nuclear norm: $$ \Vert \hat B - B\Vert_F \le K(\delta)(\Vert A - B\Vert \Vert B\Vert_*)^\frac12 \tag{1} $$ where $K(\delta) = (4 + 2\delta)\sqrt{{2}/{\delta}} + \sqrt{2 + \delta}$.
Note that we want to bound MSE, and MSE = Frobenius norm divided by $mn$. Therefore, consider $M$ estimated by thresholded SVD from Y (exactly like Lemma 3.5) — we may as well measure and bound the distance between $M$ and $Y$:
First, a simple step to regulate how many entries exactly did we observe: the proportion of observed entries, according to a beautiful Talagrand concentration inequality, will be centered around $p$ with high probability. So we might as well work with as if exactly $p$ of the entries are observed (by adjusting the bounding constants if necessary).
Assume that just about $p$ proportion of $M$ is observed and recorded into $Y$ (recall, matrix $Y$: $y_{ij} = m_{ij}$ if $(i, j)\in \Omega$ and $y_{ij} = 0$ otherwise) So since $\mathbb E[y_{ij}] = p\times m_{ij}$, define a events $E_1$ as $$ E_1:=\lbrace\Vert Y - pM\Vert \le (2 + \frac \eta2)\sqrt{np}\rbrace \tag{2} $$ Basically, this event says that under nice sampling, Y and M are sufficiently similar with high probability (Theorem 3: $\Pr[E_1] > 1 - Ce^{-cnp}$). Then if $E_1$ happen, we are able to upperbound $\hat M - M$’s Frobenius norm by combining (1) and (2):
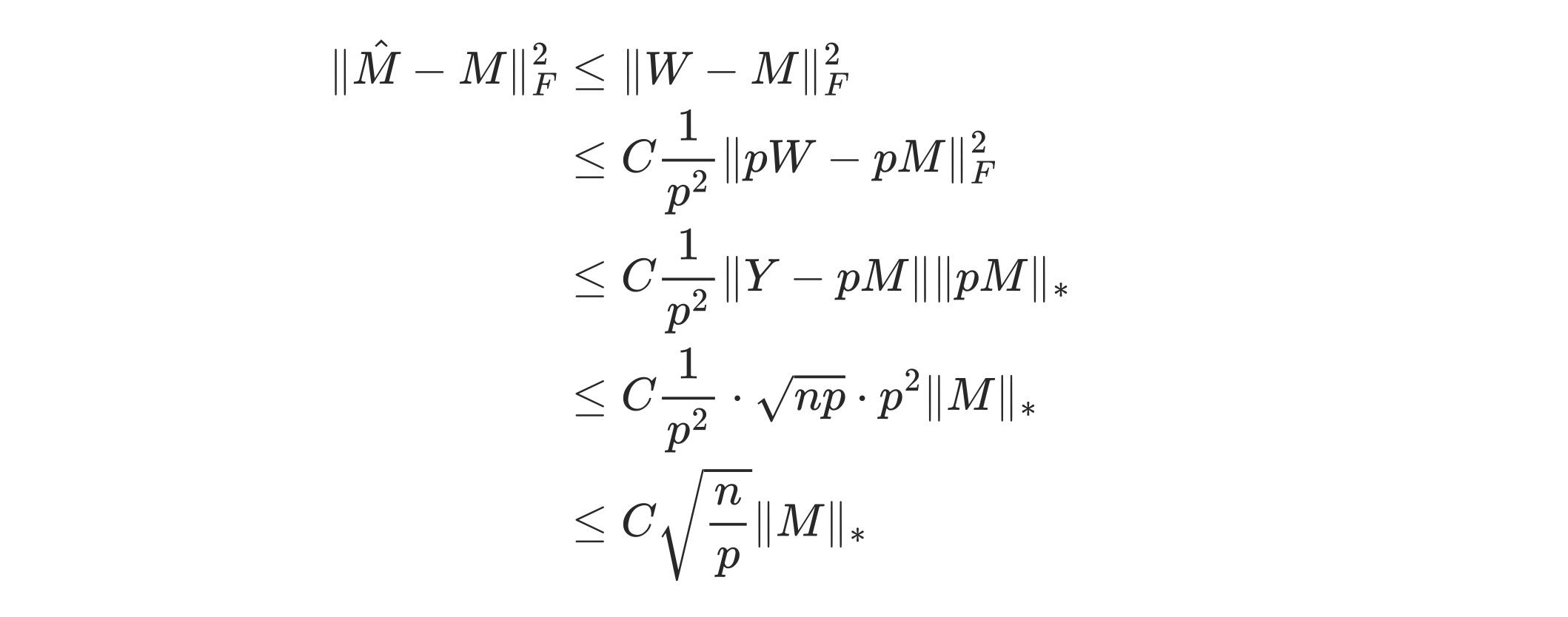
Slay.
And, recall that MSE is just 1/mn times Frobenius norm $$ \mathrm{MSE}(\hat M) = \frac1{mn}\mathbb E[\Vert \hat M - M\Vert_F^2]\le\frac{C\Vert M\Vert_*}{m\sqrt{np}} + Ce^{-cnp}. $$