The Chicago Price Theory (2019) Chapter 8 Location Choice features the following model: $$ \begin{align*} \max_{C, L, t} & \ U(C, L)\cr s.t.&\ C =\alpha + w(24 - L - t) - R(t)\cr & L, t\in [0, 24], C\ge 0. \end{align*} $$ where, $C$ is consumption (think of it as money), $L$ is leisure time, and $t$ is travel time, $R(t)$ is the rent function, assume it be decreasing. $w$ is individual’s wages. Being nice today, let’s assume $U$ is strictly concave.
Chapter 8 claimed that $R(t)$ is convex by the following reasoning: for every individual with wage $w$, the first-order optimality condition of the individual’s optimization implies $R’(t) = -w$ (hint: assume interior solution, and take derivative of the Lagrangian function w.r.t. $t$), and then, “people’s wages decrease as we move down the curve.”
Now this seems a bit tricky. Because we first assumed that every individual is optimizing over a given $R(t)$, then we obtain property of $R(t)$ out of the optimization problem. This is a circular argument.
Nevertheless, the intuition is correct to a certain degree — the claim should be formalized like this: fix any (potentially nonconvex) $R(t)$, denote as $t^{\star}(w)$ the optimal rent of individual with income $w$. Then individual’s rent choice $$ (t^{\star}(w), R(t^{\star}(w)), \quad \forall w $$ lies on a convexified $\hat R(t)$ of $R(t)$. In other words, the tenant’s optimization ourcome convexifies the rent-distance function.
Spoiler: this property is because $$ C = \alpha + w(24 - L) -\underbrace{ wt - R(t)}_{\text{linear here}}. $$
Proof
Fix $\phi$, we construct the level curve $(t, R)$. Define as $g(R, t)$ as the max utility of an individual, fixing travel time $t$ and rent $R$: $$ \begin{align*} g(R, t) = \max_{C, L} & \ U(C, L)\cr s.t.&\ C =\alpha + w(24 - L - t) - R\cr & L\in [0, 24], C\ge 0. \end{align*} $$ The level curve is then fix a $\phi$: $$ \lbrace(R, t): g(R, t) - \phi \equiv 0\tag{$\star$}\rbrace. $$ Denote as $\tilde R_\phi(t)$ the solving from $(\star)$ the implicit function of $R$ w.r.t. $t$. $U$ being strictly concave guarantees that $\tilde R_\phi(t)$ is well-defined. Now, we can obtain $$ g_R(\tilde R_\phi(t), t) \tilde R_\phi’(t) + g_t(\tilde R_\phi(t), t) = 0\Rightarrow\tilde R_\phi’(t) = -\frac{g_t}{g_R}. $$ By envelope theorem from the maximizing problem defining $g(R, t)$, let the Lagrangian be $$ \mathcal{L}(C, L, \mu; R, t) = U(C, L) + \mu[\alpha + w(24 - L - t) - R - C]. $$ Now, By the envelope theorem, $$ g_t = \frac{\partial \mathcal{L}}{\partial t} = \mu(-w), \qquad g_R = \frac{\partial \mathcal{L}}{\partial R} = \mu(-1). $$ We obtain that, every individual’s indifference curve on (Rent, time) plane is affine: $$ R_\phi’(t) = -\frac{g_t}{g_R} = -w. $$ So every individual’s optimization problem is essentially “pushing up their affine indifference curve with slope $w$ until it first tangent with $R(t)$”
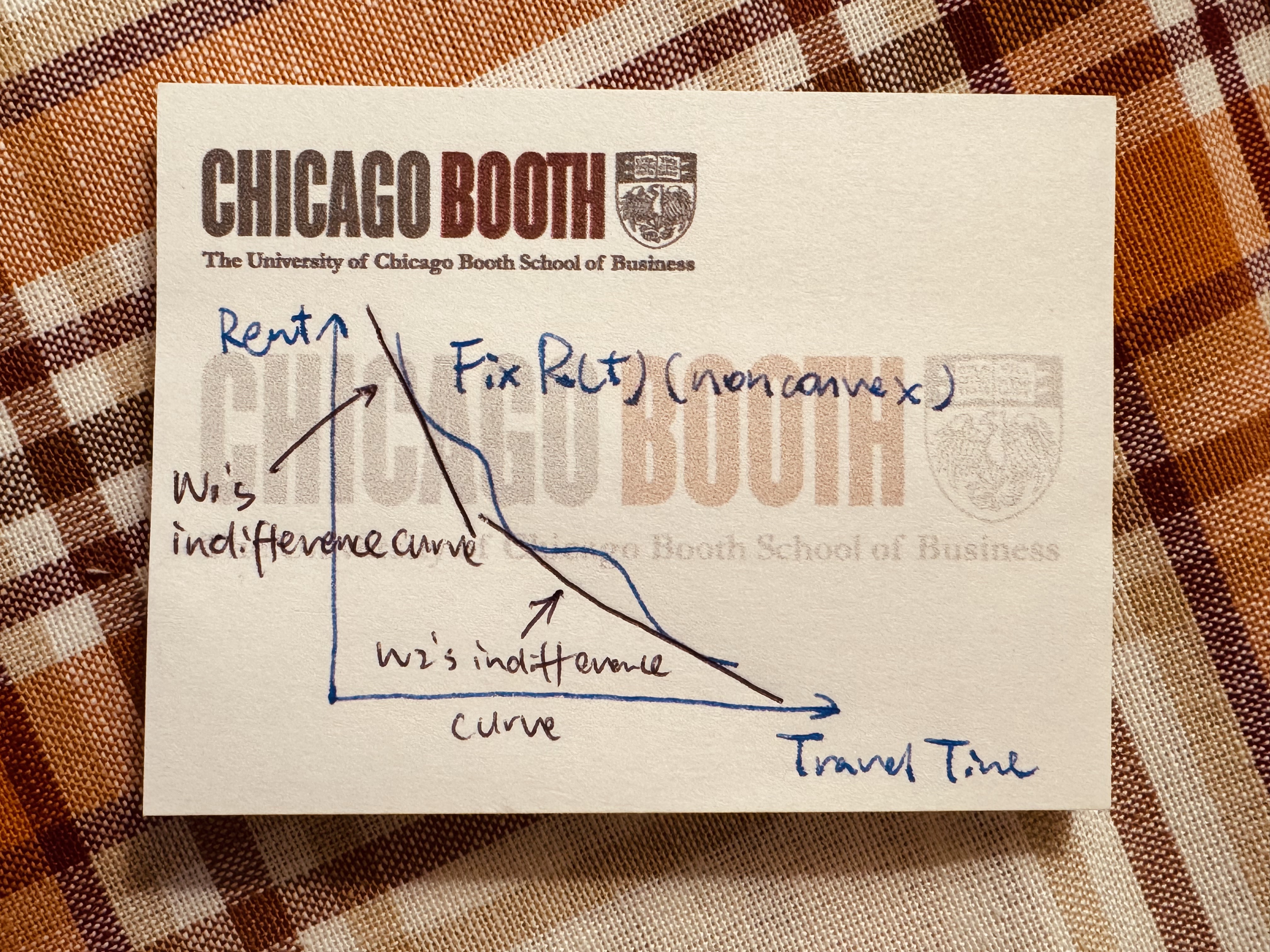
And the realized rent curve is convex.