Here’s a pretty cool and useless way to understand how to obtain the $\beta$ in linear regression.
Let’s begin with (real valued) Hilbert space, $\mathcal H$ which comes with inner product $\lang \cdot, \cdot\rang$ that are symmetric, linear and positive definite. (Might as well think classical $x, y\in \R^m$ and $\lang x, y\rang = x^Ty = \sum_{i \in [m]}x_iy_i$ in standard linear algebra)
Now suppose we are given $y\in \mathcal H$ and $X := [x_1, x_2, \ldots, x_N]\in \mathcal H^N$. The way to “project” $y$ onto $x$ is
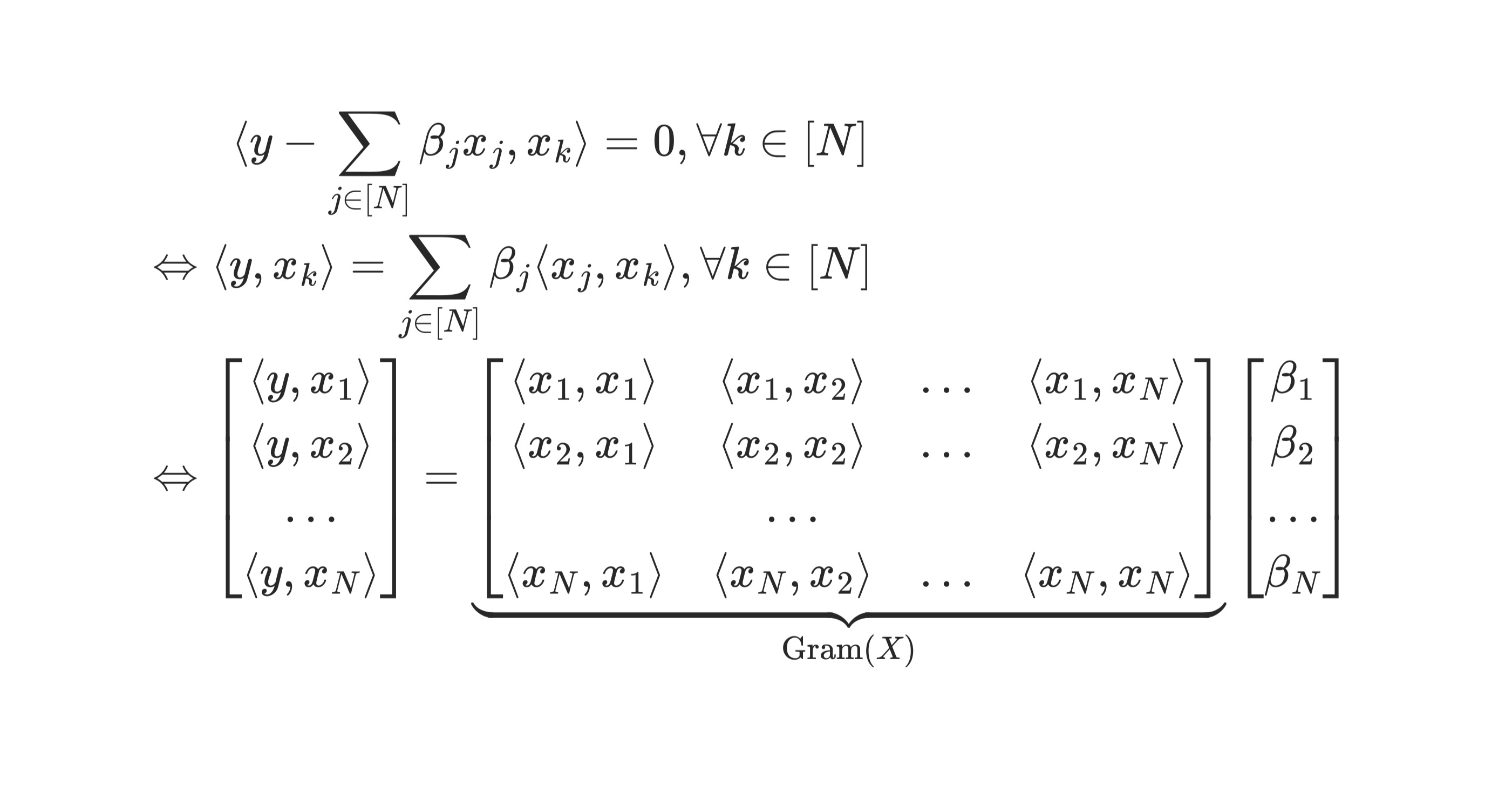
Slay.
Now this is a linear system, and we can always find $\beta = \text{Gram}(X)^{-1} [\lang y, x_k\rang]_{k\in [N]}$ — whatever $x$ and $y$ actually are, as long as $\text{Gram}(X)$ is invertible. Note that $\beta$ minimizes (proof hint: inner product is linear so we can take derivative and move it out)
$$ \beta = \arg\min_{\hat \beta}\ \lang y - \sum_{j\in [N]}\hat \beta_j x_j, \ y - \sum_{j\in [N]}\hat \beta_j x_j\rang $$
Now, consider the space of random variable $X, Y\in \R$ with finite second moment, denote as $l^2$. Let their inner product be $\lang X, Y\rang = \text{Cov}(X, Y)$, it does satisfy symmetric, linear and positive definite, makes $l^2$ a Hilbert space.
Consider general linear regression problem, $Y \in \R$ and $\vec X = [X_1, \ldots, X_N]^T\in \R^N$ are random variables. We obtain $\text{Gram}(\vec X)$
$$ \text{Gram}(\vec X) = {\begin{bmatrix} \lang X_2, X_1 \rang & \lang X_2, X_2 \rang & \ldots & \lang X_2, X_N\rang\cr \lang X_1, X_1 \rang & \lang X_1, X_2 \rang & \ldots & \lang X_1, X_N\rang\cr & \ldots & \cr \lang X_N, X_1 \rang & \lang X_N, X_2 \rang & \ldots & \lang X_N, X_N\rang\cr \end{bmatrix}} := \text{Cov}[\vec X\vec X^T]. $$
And $$ \begin{bmatrix} \lang Y, X_1\rang\cr \lang Y, X_2\rang\cr \ldots\cr \lang Y, X_N\rang \end{bmatrix} = \begin{bmatrix} \text{Cov} (Y, X_1)\cr \text{Cov} (Y, X_2)\cr \ldots\cr \text{Cov} (Y, X_N)\cr \end{bmatrix} := \text{Cov}(\vec X Y) $$ Therefore, $$ \beta =(\text{Cov}[\vec X\vec X^T])^{-1}\text{Cov}(\vec X Y) $$ minimizes $\text{Cov}(Y - \vec X^T \beta, Y - \vec X^T \beta) = \text{Var}(Y - \vec X^T \beta)$. Viola.
A hand-waving remark: recall that in linear regression $\beta =\mathbb{E}[\vec X\vec X^T]^{-1}\mathbb{E}[\vec X Y]$. This is because we add an intercept explicitly and this “centers” $X$ and $Y$.