Professor Aumann’s most highly cited paper “AGREEING TO DISAGREE” only has four pages…

Slay.
Here’s how I understand Aumann’s common knowledge:
Let the state of the world be a finite set $ \Omega $. Each agent $ i $ has an information structure represented by a partition $ \mathcal{P}_i $ over $ \Omega $. For each state $ w \in \Omega $, let $ P_i(w) \in \mathcal{P}_i $ be the element of the partition that contains $ w $. For simplicity, we consider two agents, but the results extend naturally to any number of agents.
Definition (Common Knowledge of an Event) An event $ E \subseteq \Omega $ is common knowledge at state $ w $ if the coarsest common refinement (the meet) of $ \mathcal{P}_1 $ and $ \mathcal{P}_2 $, denoted by $ \mathcal{P} = \mathcal{P}_1 \wedge \mathcal{P}_2 $, satisfies $$ \mathcal{P}(w) \subseteq E. $$
That is, within the finest partition cell consistent with both players’ information, the event $ E $ holds everywhere.
This notion extends naturally to posterior beliefs about an event.
Definition (Common Knowledge of Posteriors) For an event $ A \subseteq \Omega $, define each player’s posterior as
$$ X_i(w) = \Pr[A \mid P_i(w)]. $$We say that player $ i $’s posterior $ q_i $ on $ A $ is common knowledge at state $ w $ if $$ \forall w’ \in \mathcal{P}(w): \quad \Pr[A \mid P_i(w’)] = q_i. $$
In words, within the meet cell containing $ w $, each agent’s posterior remains constant.
Aumann’s Agreement Theorem
Under a common prior $ \Pr $ and Bayesian updating, if at state $ w $ it is common knowledge that $$ \Pr[A \mid P_1(w)] = q_1 \quad \text{and} \quad \Pr[A \mid P_2(w)] = q_2, $$ then $$ q_1 = q_2. $$
In other words, two rational agents with a common prior cannot “agree to disagree” when their posteriors are common knowledge.
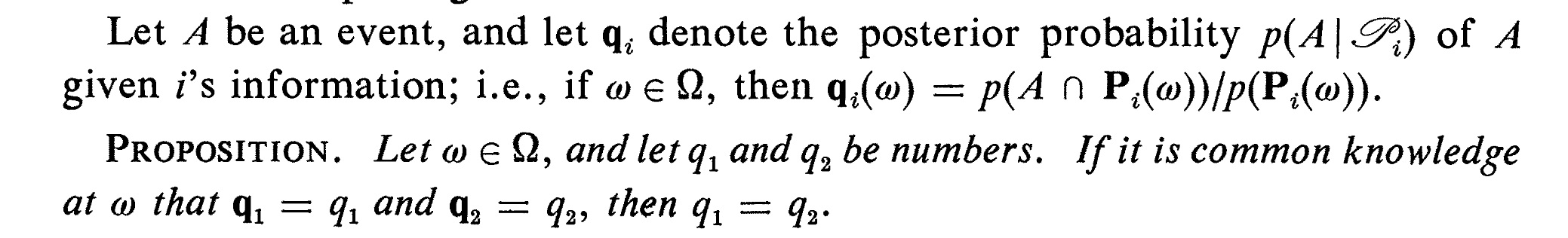
Slay.
Reference
Aumann, Robert J. “Agreeing to Disagree.” The Annals of Statistics, vol. 4, no. 6, 1976, pp. 1236–39. JSTOR, http://www.jstor.org/stable/2958591. Accessed 17 Oct. 2025.
Quint, D. (n.d.). Lecture 3 [PDF lecture notes]. University of Wisconsin–Madison. [https://users.ssc.wisc.edu/~dquint/econ698/lecture%203.pdf#](https://users.ssc.wisc.edu/~dquint/econ698/lecture 3.pdf)