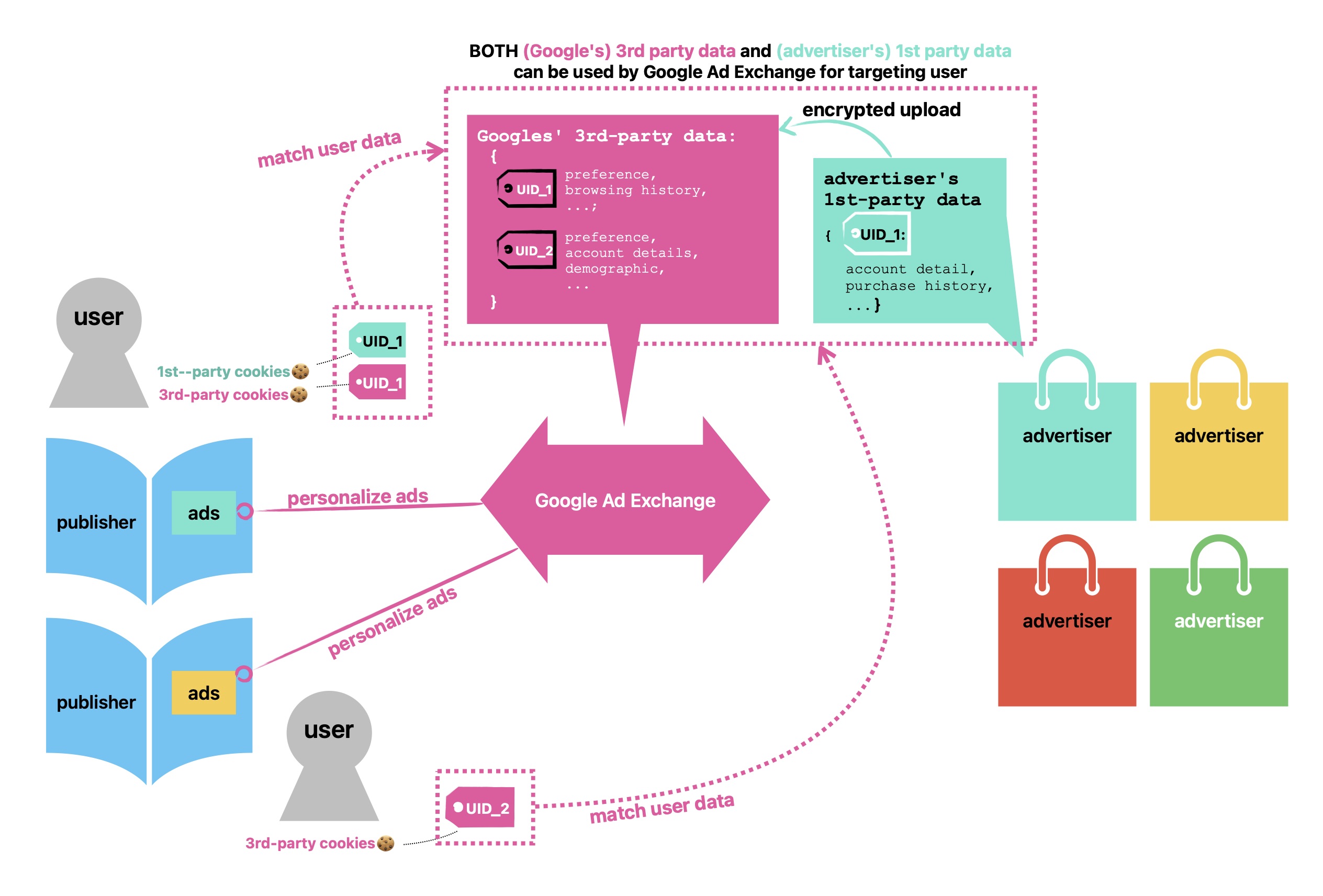
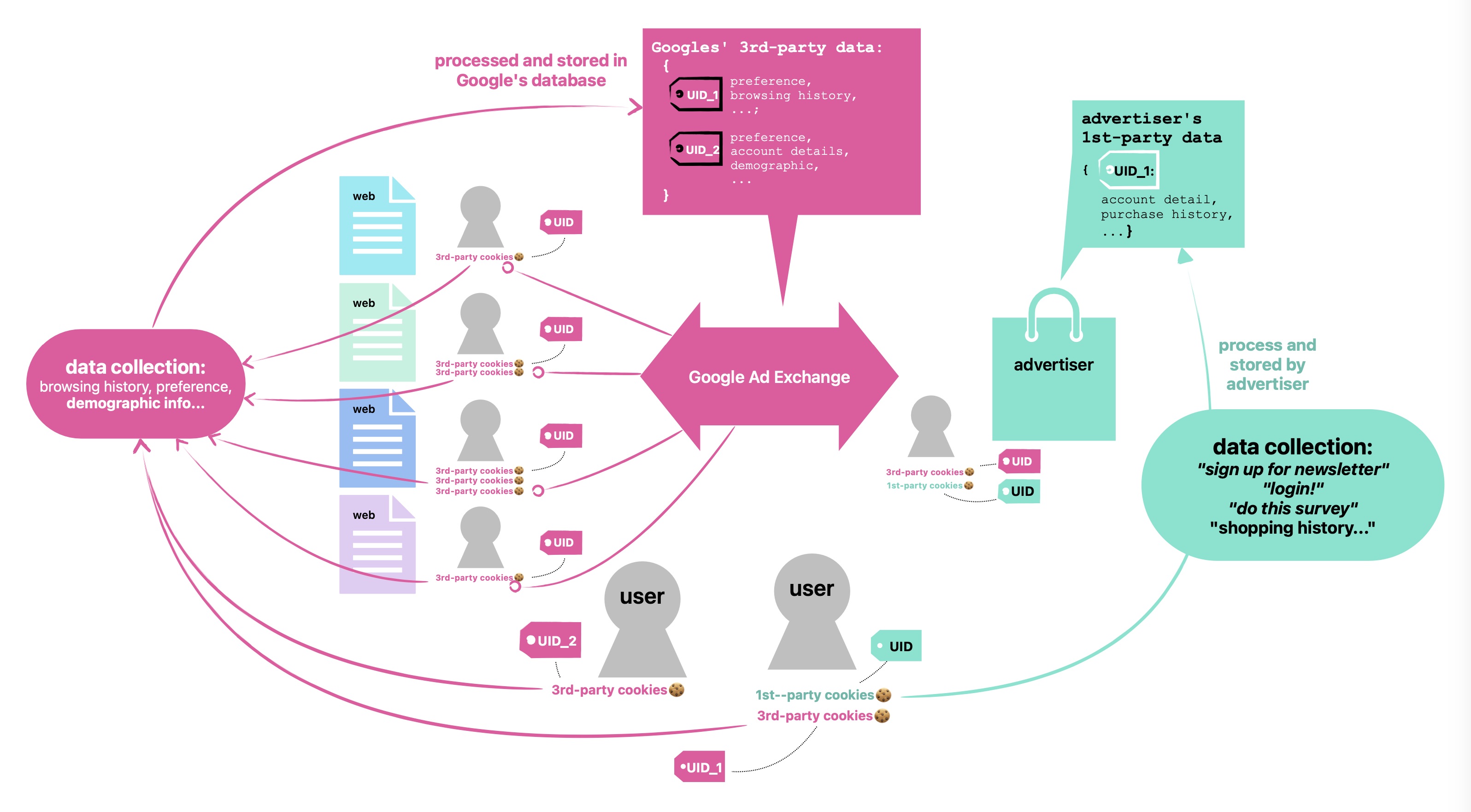
Cookie Box | Content for the Cookie series
I’m excited to present the Cookie series—a collection of everything you need to know about internet Cookies. This Cookie series is a one-stop guide to understanding everything about internet cookies—what they are, how they work, and why they matter. Let’s open and see what’s inside the Cookie Box! technical basics What are Cookies Who collect data via Cookies, and how? Cookie syncing How data is used for ad targeting regulations The rule for cookies GDPR and CCPA: the major regulation landscape China’s stance Industry Trends and Reactions, staring from July 2024 market landscape The Value of Cookies AdTech Landscape Demand-Side Platforms Market size and market shares of Ad-Tech industry the key when buying ads — targeting Data brokers Google Gossip Surprising News: Google stopped decaprecating Cookies the Cookies Confusion and the Antitrust Avalanche extras supplementary materials ...